masm multiplication method

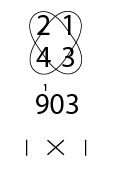
Learning the patterns from the line multiplication method we can establish a new more efficient way to multiply numbers together and skip redundancies.
Looking at this first example of 21 x 43 we always start on the right by multiplying the first numbers on the right columm. So 1 x 3 equals 3. Then we multiply the numbers circled to the left so 2 x 3 and 4 x 1. so 6 and 4. Add the numbers up for 10. keep 0 and carry the 1.
For the last number we multiply the two numbers on the left column so 2 x 4 equals 8. Add the 1 carried for 9 which equals 903.
The lines at the bottom indicate the multiplication pattern used.
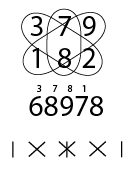
In this next example we are multiplying 379 x 182. We start by multiplying 9 x 2 on the right column for 18. Carry the 1 and keep the 8.
Next we follow the next pattern lines bellow so we would do 7 x 2 and 8 x 9. So 14 and 72. Add those for 86. Add the 1 for 87. Carry the 8 and keep the 7.
The next line pattern is to multiply the numbers circled. So 3 x 2, 7 x 8, and 1 x 9. So 6 + 56 + 9 equals 71. Add the 8 for 79. Carry the 7 and keep the 9.
The next numbers would be 3 x 8 + 1 x 7 which equals 31. Add the 7 for 38. Carry the 3 and keep the 8.
And then we multiply the last two numbers 3 x 1 equals 3 and add 3 for 6.

As the numbers increase so does the line multiplication pattern.
Here we have an example of 1433 times 2254.
Again we start by multiplying the first numbers on the right 3 x 4 for 12. Carry the 1 and keep the 2.
Next we multiply 3 x 4 and 5 x 3. 12 + 15 for 27. Add the 1 for 28. Carry the 2 and keep the 8.
Next multiply 4 x 4, 2 x 3, and 3 x 5. 16 + 6 + 15 which equals 37. Add 2 for 39. Carry the 3 and keep the 9.
Next multiply 1 x 4, 2 x 3, 4 x 5, 2 x 3 for 4 + 6 + 20 + 6 which equals 36. Add 3 for 39. Carry the 3 and keep the 9.
Next multiply 1 x 5, 2 x 3, and 4 x 2. Then 5 + 6 + 8 which equals 19. Add 3 for 22. Carry the 2 and keep 2.
Next multiply 1 x 2 + 2 x 4 which gives us 10. Add 2 for 12. Carry the 1 and keep 2.
Then multiply the last two numbers 1 x 2 for 2. Add 1 for 3. Then write numbers back 3229982.

Using this approach we can find the line patterns when multiplying smaller numbers with larger ones.
In this example we do not exceed the 2 line pattern.
To start we multiply the first numbers 7 x 1 for 7.
Then we multiply 9 x 1 and 7 x 4 for 9 + 28 which equals 37. Carry the 3 and keep the 7.
Then we continue this similar pattern. The next numbers would be 2 x 1 and 4 x 9. So 2 + 36 which equals 38. Add 3 for 41. Carry the 4 and keep the 1.
The next one would be the numbers circled so 6 x 1 and 4 x 2. So 6 + 8 for 14. Add 4 for 18. Carry the 1 and keep the 8.
Then again 5 x 1 and 4 x 6. So 5 + 24 for 29. Add 1 for 30. Carry the 3 and keep 0.
Then the last two numbers 5 x 4 for 20. Add 3 for 23. Then combine the numbers back for 2308177.

For this last example since the lowest number is only one digit then the highest line combo is one.
In this case we would start with 8 x 9 for 72. Carry the 7 and keep the 2.
Then we multiply 7 x 9 for 63. Add 7 for 70 and then combine with the first number for 702.
This method can be used with decimals as well which is great and saves a lot of redundant processes when multiplying large numbers.